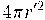Volums us Àrees

Amb l'ajuda d'un full de càlcul i les funcions PI(), ARRELQ() i de l'operador potència (cal prémer dos cops la tecla de l'accent circumflex ^ ), avalua les superfícies dels tres cossos geomètrics de la imatge.
Disposem d'un cub d'aresta = 1 m, que emmagatzema 1m³ de líquid, construeix un cilindre de la mateixa alçada h = 1m i un radi r que li confereixi la mateixa capacitat i així mateix, una esfera amb el radi r' necessari per contenir el m³.
Finalment, dona resposta a la qüestió: Quina de les tres geometries, empraries per emmagatzemar el metre cúbic i per quin motiu? i fes la tramesa del full de càlcul que has emprat per avaluar els càlculs necessaris.
Comproveu que les superfícies corresponents són:
Superfície Cub = 6 m2
Superfície Cilindre = 5,54 m2
Superfície esfera = 4,84 m2
Hint: Trobarem els corresponents radis r i r' a partir d'imposar el volum d'1 m³ com a resultat del càlcul i després els substituirem a les expressions que ens permeten calcular les respectives superfícies.
Volum Cilindre =  = 1 d'on
= 1 d'on 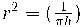 i donat que h=1 tenim
i donat que h=1 tenim ![r = \frac{1}{ \sqrt[]{\pi} } r = \frac{1}{ \sqrt[]{\pi} }](https://aulari.joseptous.org/filter/tex/pix.php/4690d39a1be82d75a044daef52d0e8bf.gif)
Volum i radi r al full de càlcul: V = pi()*r^2*h i r = (1/ arrelq(pi()))
Superficie al full de càlcul: S = 2*pi()*r^2 + 2*pi()*r*h
Volum Esfera =  = 1 d'on
= 1 d'on 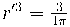 i donat que ens interessa
i donat que ens interessa 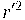 tenim
tenim ![r'^2 = \sqrt[3]{ (\frac{3}{4\pi} )^2} r'^2 = \sqrt[3]{ (\frac{3}{4\pi} )^2}](https://aulari.joseptous.org/filter/tex/pix.php/63da7e37f8e9c25f9e3cb8f5fd68fa22.gif)
Volum i radi 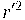 al full de càlcul: V = (4/3)*pi()*r'^3 i r'^2= (3/(4*pi()))^(2/3)
al full de càlcul: V = (4/3)*pi()*r'^3 i r'^2= (3/(4*pi()))^(2/3)
Superfície al full de càlcul: S = 4*pi()*r'^2
S'està qualificant Trameses
Rúbrica per valorar la tasca opcional de Volums vs Àrees.
| Enunciat |
| ||||
| Càlcul Superfícies a partir d'un volum determinat. |
| ||||
| Resposta a la qüestió formulada. |
|