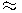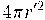Kachel: Geometria. | Matemàtiques3rESO (Lluís) | Aulari

Agenda Aules Digitals Recursos Tous Qüestionaris TR

Geometria.

Unitats 7, 8 i 9 1r Parcial

El lloc geomètric és el conjunt de tots els punts que compleixen una propietat geomètrica determinada.

Hi ha magnituds de les quals, a més del valor numèric, hem de saber la direcció i el sentit: són les magnituds vectorials.

Dos punts del pla, A i B, determinen un vector fix AB, en el qual A és l'origen i B és l'extrem.

La distància entre A i B (longitud del segment AB) s’anomena mòdul del vector, i la recta que passa per A i B és la direcció del vector. El sentit és el que va de A a B.

Els poliedres són cossos geomètrics tancats limitats per polígons. Poden ser còncaus o convexos.
Els poliedres convexos verifiquen la fórmula d’Euler: C + V = A + 2, en què C = nre. de cares, V = nre. de vèrtexs i A = nre. d’arestes.
- Llocs geomètrics. Àrees i perímetres.
  
  El lloc geomètric és el conjunt de tots els punts que compleixen una propietat geomètrica determinada.
- Formulari àrees i volums
- Xuleta Unitat 7
  
  Confeccioneu un document Google Docs amb un recull dels conceptes i definicions claus de la unitat 7. Haureu de compartir el document amb l'opció d'enllaç i disposeu d'un espai de tasca en línia on me'l podeu indicar per accedir-hi.
  
  Hint: Recordeu que molt probablement, el profe us la deixi emprar o no, quan fem el parcial pertinent. Fet que no us ha d'eximir d'estudiar amb normalitat.
- Llocs geomètrics ( I ) amb Geogebra
  
  Amb l'ajuda del programari Geogebra confecciona un document Google Docs i comparteix-lo en línia amb l'opció d'enllaç, on es reflecteixin les rectes i els punts notables dels triangles (Circumcentre (Mediatrius), Incentre(Bisectrius), Ortocentre(Altures), Baricentre(Medianes) i recta d'Euler (Tots els llocs menys l'incentre).
  
  NOTA: Disculpeu el soroll de fons, és una font d'alimentació avariada, "... en casa del herrero ... "
- Dibuixem polígons amb Scratch
  Cal interpretar aquesta tasca com un recurs per verificar l'àrea d'un polígon regular que ens puguem trobar en algun exercici.
  
  L'objectiu d'aquesta activitat és veure com podem generar polígons regulars interactuant amb l'usuari.
  
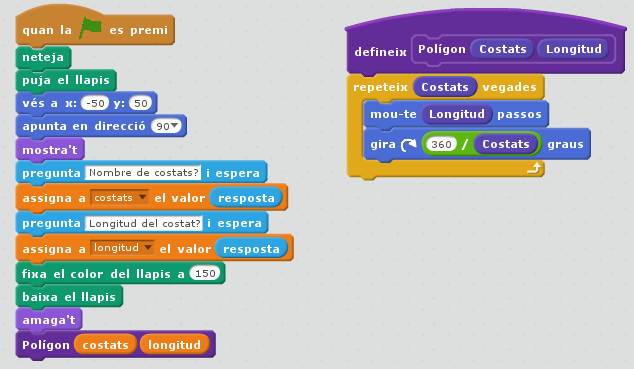
  Demanem a l'usuari el nombre de costats i la seva longitud. Emmagatzemem les entrades a les variables globals: Costats i Longitud
  
  Desplaçarem el nostre "llapis", la longitud indicada i a continuació girarem 360°/Costats (a dreta o esquerra) els graus necessaris per encarar el nou tram, repetint el procediment, tantes vegades com el total de costats indicats per l'usuari.
  
  Cal contemplar altres aspectes com netejar la pantalla i decidir la posició inicial de l'animació.
  
  Com ho faries per indicar l'àrea del polígon regular dibuixat?
  
  Les magnituds que ens interessen
  
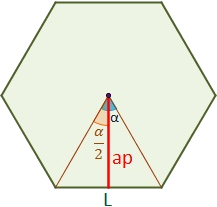
  Les fórmules, necessitaràs crear tres variables. Angle, Apotema i Àrea.
  
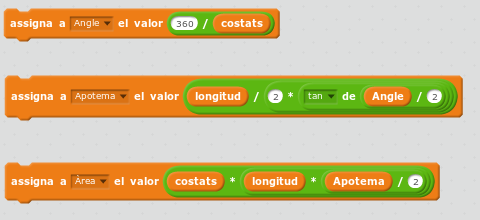
  I finalment hauràs de tornar a mostrar el gatet i dir el resultat de l'àrea calculada.
  
  Indica l'enllaç a la teva tasca Scratch i assegura't que l'has compartida correctament.
- Fitxer Scratch
  
  Càlcul de l'àrea d'un polígon regular amb Scratch
- Moviments i Semblances.
  
  Ho treballarem a l'espai del Geogebra
- Xuleta Unitat 8
  
  Confeccioneu un Google Docs amb un recull dels conceptes i definicions claus de la unitat 8. Haureu de compartir el document amb l'opció d'enllaç i disposeu d'un espai de tasca en línia on me'l podeu indicar per accedir-hi.
  
  Hint: Recordeu que molt probablement, el profe us la deixi emprar o no, quan fem el parcial pertinent. Fet que no us ha d'eximir d'estudiar amb normalitat.
- Translacions, Simetries, Homotècies, Teorema de Tales i tal ...
  
  Consulteu la secció de transformacions del manual de Geogebra.
  
  Per anar agafant idees i ampliar les nostres habilitats amb el Geogebra, doneu un cop d'ull a aquest SlideShare ...
- Transformacions geomètriques amb Geogebra
  Amb l'ajuda del programari Geogebra confecciona un document Google Docs on es reflecteixin els següents ítems:
  
  Un vector indicant les seves característiques: coordenades, direcció, sentit, mòdul.
  
  Un exemple de translació d'un objecte amb el vector de l'apartat 1.
  
  Un exemple de rotació horària i antihorària.
  
  Un d'una simetria axial i una altra central.
  
  Una homotècia d'un pentàgon regular, de factor k=3.
  
  PD: En els apartats 2, 3, 4 i 5 cal indicar les característiques de les transformacions geomètriques efectuades.
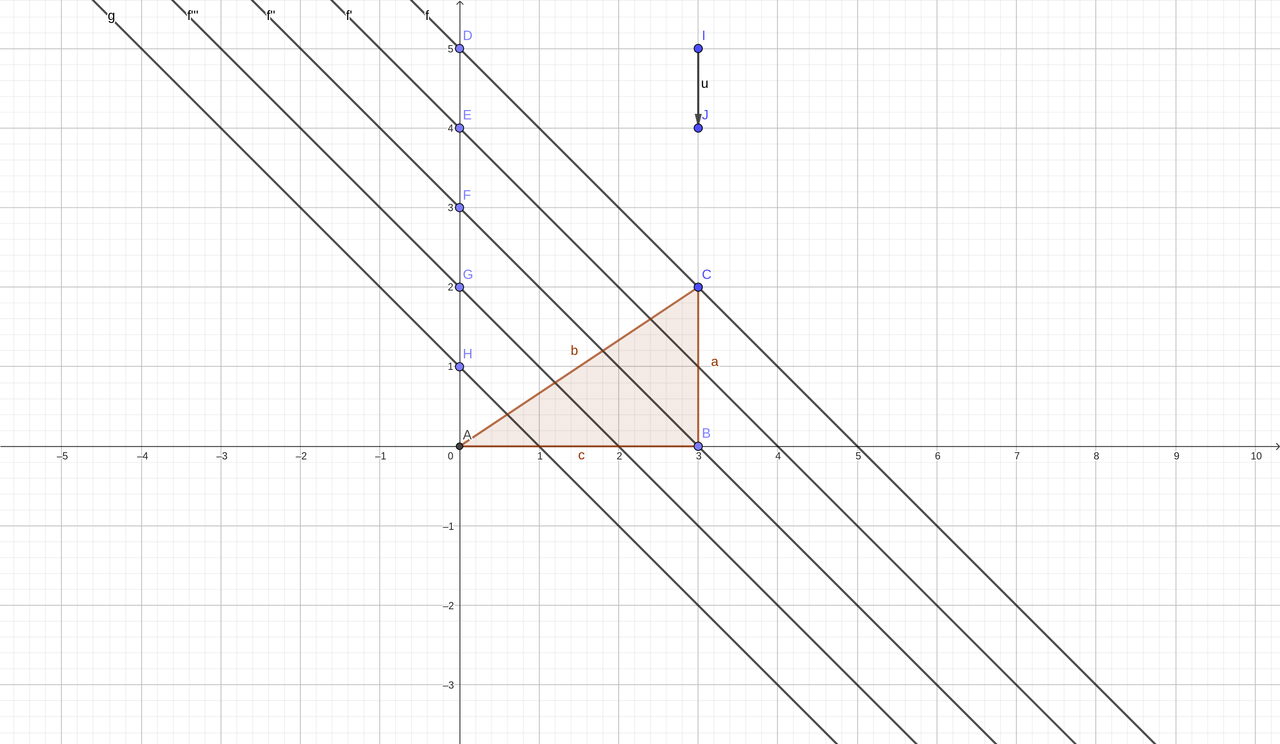
- Construïm i dividim un segment gràficament
  
  Construeix gràficament, llegeixis emprant el mètode d'assimilar-lo a la hipotenusa d'un triangle rectangle, un segment de longitud $\sqrt[2]{26}$ .
  
  Un cop aconseguit, divideix-lo en cinc parts iguals, fent servir algun dels dos mètodes explicats amb el Geogebra.
  
  Finalment, fes la tramesa en línia de l'enllaç a la teva tasca Geogebra.
  
  Hint:
- Camí a l'escola (Escala Gràfica)
  
  Aquesta tasca us demana que feu un càlcul aproximat, de la distància que separa el vostre domicili habitual de l'escola (C/Begur 12, Barcelona), utilitzant les tècniques explicades a classe i confrontant els resultats amb els que us ofereix el mateix Google Maps.
  
  A la imatge i a la diagonal inferior dreta, podem localitzar l'escala gràfica que el Maps redimensiona de forma dinàmica.
  
  L'objectiu, opcional per aquells que disposeu d'impressora, consistiria a imprimir el mapa amb la ruta i l'escala, resseguint la primera amb un cordill que posteriorment mesuraríem amb l'ajuda d'un regle i faríem els càlculs pertinents amb l'escala proporcionada per estimar la distància real que separa les nostres llars, de l'escola.
  
  Tots plegats aprendrem a fer la mesura amb l'ajuda de l'Inkscape un programari de disseny vectorial gratuït, multiplataforma, lliure i de codi obert.
- Àrea de Collserola
  
  Aquesta tasca us demana que feu un càlcul aproximat, de l'àrea del Parc Nacional de Collserola, utilitzant les tècniques explicades a classe
  
  i confrontant els resultats amb els que us ofereixen d'altres fonts d'internet.
  
  A la imatge i a la diagonal inferior dreta, podem localitzar l'escala gràfica que el Google Maps redimensiona de forma dinàmica.
  
  L'objectiu, consisteix en incorporar la imatge de referència al Geogebra i fer el recobriment del parc amb una graella de dimensiones conegudes que ens permeti fer una estimació de la superfície d'aquest.
  
  Finalment ho podem comparar amb els resultats obtinguts emprant el propi Google Maps
  
  Tramesa: Dos enllaços, l'un al projecte Geogebra compartit en línia amb la graella amb el recompte dels punts per defecte i per excés (els podeu canviar de color, de fet, els heu de canviar de color) i l'altre a una comparativa (en línia, Google Docs) dels resultats obtinguts amb els del Google Maps i les dades de la Wikipèdia o fins i tot comparant-ho amb la resposta del ChatGPT i amb la pròpia obtinguda amb el mètode de la graella.
  
  Hint: Podeu automatitzar la creació de la graella emprant la funció Seqüència o Seqüència del Geogebra.
  
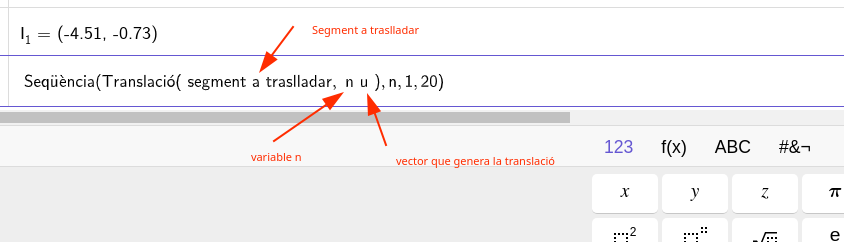
  Hint: Teniu una graella dinàmica a la vostra disposició a https://www.geogebra.org/classic/ya4nnatr (cal tenir la sessió iniciada a Geogebra per poder accedir-hi).
- Graella.ggb
  
  Si l'enllaç precedent us dona problemes, podeu descarregar-vos el fitxer Geogebra (Graella.ggb) d'aquesta entrada amb la mateixa graella dinàmica.
- Cossos geomètrics.
  
  Ho treballarem a l'espai del Geogebra
- Xuleta Unitat 9
  
  Confeccioneu un document amb Google Docs amb un recull dels conceptes i definicions claus de la unitat 9. Haureu de compartir el document amb l'opció d'enllaç i disposeu d'un espai de tasca en línia on me'l podeu indicar per accedir-hi.
  
  Hint: Recordeu que molt probablement, el profe us la deixi emprar o no, quan fem el parcial pertinent. Fet que no us ha d'eximir d'estudiar amb normalitat.
- Cossos geomètrics ( I ) amb Geogebra
  
  Amb l'ajuda del programari Geogebra confecciona un document, Google Docs on es reflecteixin , correctament identificats, els poliedres regulars (Sòlids Platònics) i els seus desplegaments.
  
  Així mateix, comproveu per cadascun d'ells que es compleix la Llei d'Euler: Cares + Vèrtexs = Arestes + 2
- Volums us Àrees
  
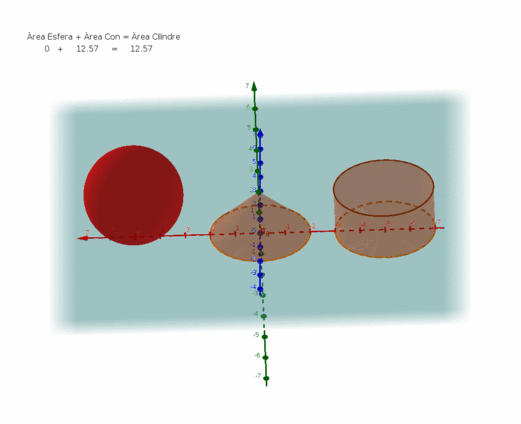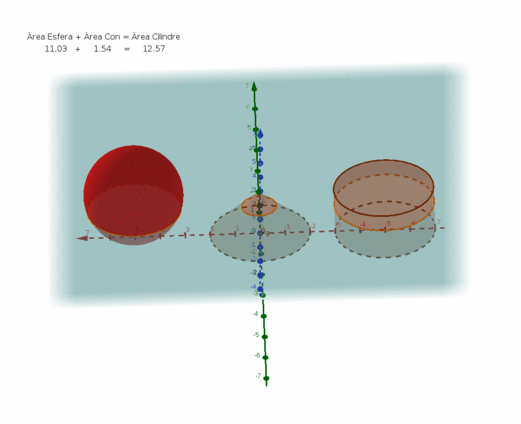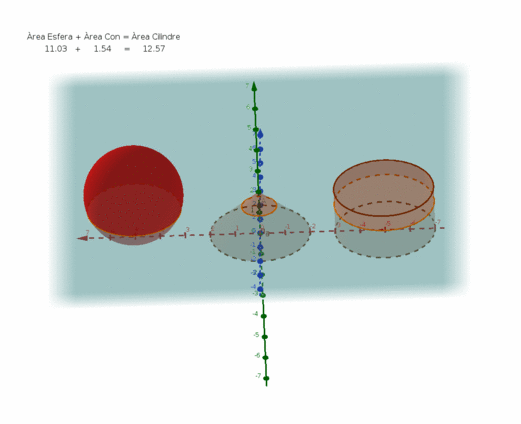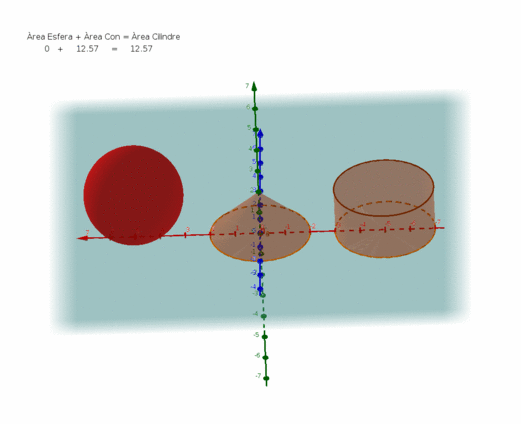
  Amb l'ajuda d'un full de càlcul i les funcions PI(), ARRELQ() i de l'operador potència (cal prémer dos cops la tecla de l'accent circumflex ^ ), avalua les superfícies dels tres cossos geomètrics de la imatge.
  
  Disposem d'un cub d'aresta = 1 m, que emmagatzema 1m³ de líquid, construeix un cilindre de la mateixa alçada h = 1m i un radi r que li confereixi la mateixa capacitat i així mateix, una esfera amb el radi r' necessari per contenir el m³.
  
  Finalment, dona resposta a la qüestió: Quina de les tres geometries, empraries per emmagatzemar el metre cúbic i per quin motiu? i fes la tramesa del full de càlcul que has emprat per avaluar els càlculs necessaris.
  
  Comproveu que les superfícies corresponents són:
  
  Superfície Cub = 6 m²
  
  Superfície Cilindre = 5,54 m²
  
  Superfície esfera = 4,84 m²
  
  Hint: Trobarem els corresponents radis r i r' a partir d'imposar el volum d'1 m³ com a resultat del càlcul i després els substituirem a les expressions que ens permeten calcular les respectives superfícies.
  
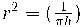  Volum Cilindre = $\pi r^2h$ = 1 d'on $r^2 = ( \frac{1}{\pi h} )$ i donat que h=1 tenim $r = \frac{1}{ \sqrt[]{\pi} }$
  
  Volum i radi r al full de càlcul: V = pi()*r^2*h i r = (1/ arrelq(pi()))
  
  Superfície Cilindre = $2 \pi r^2 + 2\pi rh$
  
  Superficie al full de càlcul: S = 2*pi()*r^2 + 2*pi()*r*h
  
  Radi Cilindre ( r ) $\approx$ 0.5642
  
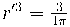  Volum Esfera = $\frac{4}{3}\pi r'^3$ = 1 d'on $r'^3 = \frac{3}{4\pi}$ i donat que ens interessa 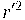$r'^2$ tenim $r'^2 = \sqrt[3]{ (\frac{3}{4\pi} )^2}$
  
  Volum i radi 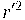$r'^2$ al full de càlcul: V = (4/3)*pi()*r'^3 i r'^2= (3/(4*pi()))^(2/3)
  
  Superfície Esfera = $4\pi r'^2$
  
  Superfície al full de càlcul: S = 4*pi()*r'^2
  
  Radi Esfera ( r' ) $\approx$ 0.6204
- Explicació càlcul del volum de l'esfera https://www.gaussianos.com/el-volumen-de-la-esfera/
  
  Exemplificant el Principi de Cavalieri amb el Geogebra.
- Aplicació del Principi de Cavalieri al cas d'una semiesfera, un con i un cilindre.
- Aplicació del Principi de Cavalieri al cas de dos cons i un cilindre
- Determinació de la separació horària